Learning Latent Space Energy-Based Prior Model

Bo Pang^*, Tian Han^*, Erik Nijkamp^*, Song-Chun Zhu, Ying Nian Wu

^* Equal contributions
University of California, Los Angeles (UCLA), USA

Abstract

The generator model assumes that the observed example is generated by a low- dimensional latent vector via a top-down network, and the latent vector follows a simple and known prior distribution, such as uniform or Gaussian white noise distribution. While we can learn an expressive top-down network to map the prior distribution to the data distribution, we can also learn an expressive prior model instead of assuming a given prior distribution. This follows the philosophy of empirical Bayes where the prior model is learned from the observed data. We propose to learn an energy-based prior model for the latent vector, where the energy function is parametrized by a very simple multi-layer perceptron. Due to the low- dimensionality of the latent space, learning a latent space energy-based prior model proves to be both feasible and desirable. In this paper, we develop the maximum likelihood learning algorithm and its variation based on short-run Markov chain Monte Carlo sampling from the prior and the posterior distributions of the latent vector, and we show that the learned model exhibits strong performance in terms of image and text generation and anomaly detection.

Paper

The publication can be obtained here.

@article{pang2020ebmprior,
  title={Learning Latent Space Energy-Based Prior Model},
  author={Pang, Bo and Han, Tian and Nijkamp, Erik and Zhu, Song-Chun and Wu, Ying Nian},
  journal={NeurIPS},
  year={2020}
}

Contributions

(1) We propose a generator model with a latent space energy-based prior model by following the empirical Bayes philosophy.
(2) We develop the maximum likelihood learning algorithm based on MCMC sampling of the latent vector from the prior and posterior distributions.
(3) We further develop an efficient modification of MLE learning based on short-run MCMC sampling.
(4) We provide theoretical foundation for learning driven by short-run MCMC.
(5) We provide strong empirical results to corroborate the proposed method.

Code

The code can be obtained here.

Experiments

Experiment 1: Image

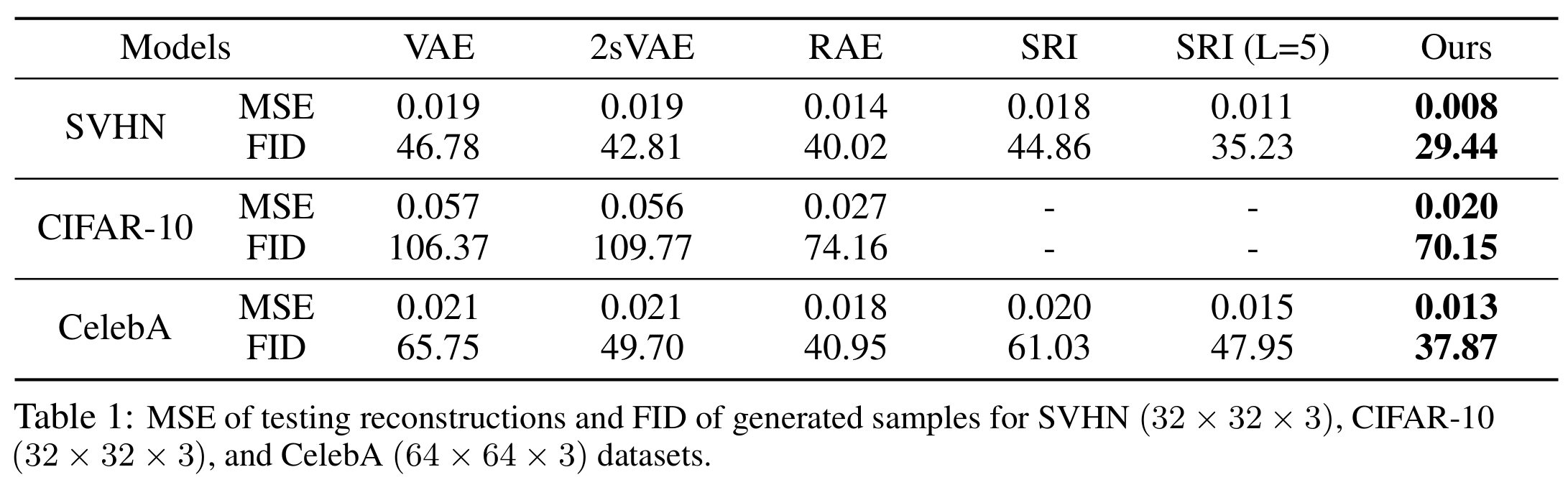
The generator network \(p_\theta\) in our framework is well-learned to generate samples that are realistic and share visual similarities as the training data. The qualitative results are shown in Figure 1. We further evaluate our model quantitatively by using Fréchet Inception Distance (FID) in the table below. It can be seen that our model achieves superior generation performance compared to listed baseline models.

Figure 1: Generated samples for SVHN \((32 \times 32)\), CIFAR-10 \((32 \times 32)\), and CelebA \((64 \times 64)\).

Experiment 2: Text

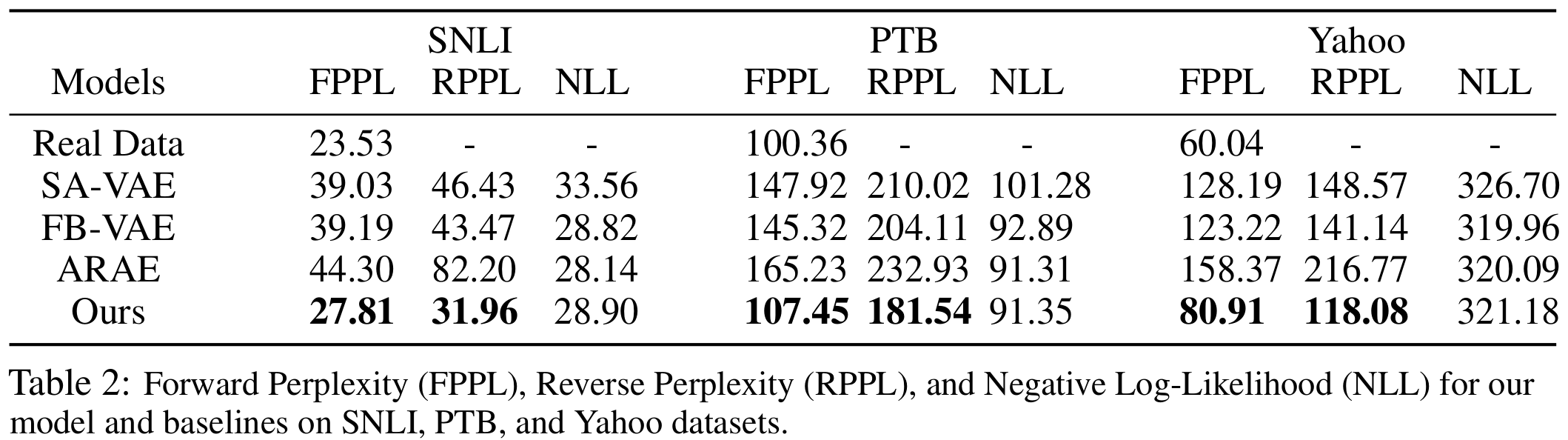
To evaluate the quality of the generated samples, we recruit Forward Perplexity (FPPL) and Reverse Perplexity (RPPL). FPPL is the perplexity of the generated samples evaluated under a language model trained with real data and measures the fluency of the synthesized sentences. RPPL is the perplexity of real data (the test data partition) computed under a language model trained with the model-generated samples. Prior work employs it to measure the distributional coverage of a learned model, \(p_\theta(x)\) in our case, since a model with a mode-collapsing issue results in a high RPPL. FPPL and RPPL are displayed in Table 2. Our model outperforms all the baselines on the two metrics, demonstrating the high fluency and diversity of the samples from our model.

Experiment 3: Analysis of latent space

We examine the exponential tilting of the reference prior \(p_0(z)\) through Langevin samples initialized from \(p_0(z)\) with target distribution \(p_\alpha(z)\). As the reference distribution \(p_0(z)\) is in the form of an isotropic Gaussian, we expect the energy-based correction \(f_\alpha\) to tilt \(p_0\) into an irregular shape like some shallow local modes. Therefore, the trajectory of a Markov chain initialized from the reference distribution \(p_0(z)\) with well-learned target \(p_\alpha(z)\) should depict the transition towards synthesized examples of high quality while the energy fluctuates around some constant. Figure 2 depicts such transitions for CelebA, which is based on a model trained with \(K_0 = 40\) steps. The quality of synthesis improves significantly with increasing number of steps.

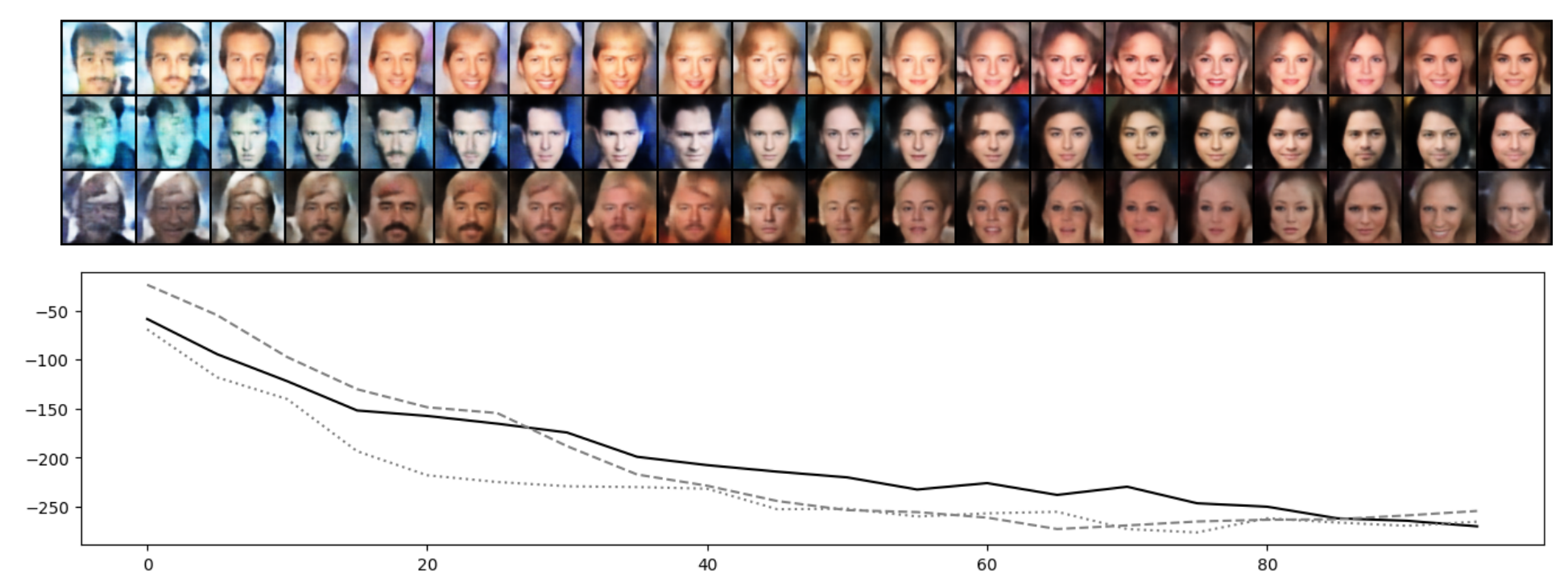
Figure 2: Transition of Markov chains initialized from \(p_0(z)\) towards \(\tilde{p}_{\alpha}(z)\) for \(K_0'=100\) steps. Top: Trajectory in the CelebA data-space. Bottom: Energy profile over time.

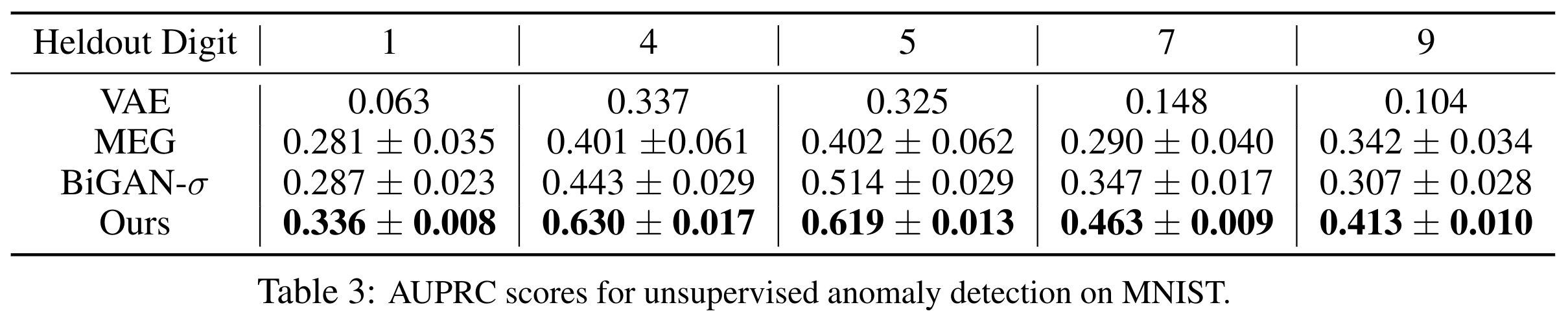
Experiment 4: Anomaly detection

If the generator and EBM are well learned, then the posterior \(p_\theta(z|x)\) would form a discriminative latent space that has separated probability densities for normal and anomalous data. Samples from such latent space can then be used as discriminative features to detect anomalies. We perform posterior sampling on the learned model to obtain the latent samples, and use the unnormalized log-posterior \(\log p_\theta(x, z)\) as our decision function.

Experiment 5: Scalability

We have also explored avenues to improve training speed and found that a PyTorch extension, NVIDIA Apex, is able to improve our model training 2.5 times. We test our method with Apex training on a larger scale dataset, CelebA \( (128 \times 128 \times 3) \). The learned model is able to synthesize examples with high fidelity.

Acknowledgements

The work is supported by NSF DMS-2015577, DARPA XAI N66001-17-2-4029, ARO W911NF1810296, ONR MURI N00014-16-1-2007, and XSEDE grant ASC170063. We thank NVIDIA for the donation of Titan V GPUs.